정렬
가지고 있는 자료를 사용하기 편하도록 정렬하려면 어떤 방법이 있을까? 이때 고민해 볼 수 있는 것이 정렬 알고리즘이다.
우선 정렬 Sort이란 순서 없이 배열된 자료를 작은 것부터 또는 큰 것부터 오름차순, 내림차순으로 재배열(재배치)하는 것이다.
여기서 재배열을 하는 기준을 어떻게 정하나인데, 가게를 예를 들면 유통기한 순으로 물건을 다시 진열하거나, 우리가 살면서 해야 할 일을 적을 때도 마찬가지이다. 이처럼 일상생활에서 자주 사용하는데....
자료를 정렬하는데 사용하는 기준이 되는 특정 값(유통기한, 날짜 등)을 켜라고 한다. 따라서 우리는 그 키를 기준으로 정렬하면 크기가 키가 된다.

정렬 방식의 분류
| 기준 | 정렬 방식 | 설명 |
| 실행 방법 | 비교식 정렬 Comparative Sort | 비교할 각 키값을 한 번에 두 개씩 비교하여 교환함으로써 정렬을 한다. |
| 분배식 정렬 Distribute Sort | 키값을 기준으로 하여 자료를 여러 개의 부분 집합으로 분해하고, 각 부분 집합을 정렬함으로써 전체를 정렬한다. | |
| 정렬 장소 | 내부 정렬 Internal Sort | 컴퓨터 메모리 내부에서 정렬 |
| 외부 정렬 External Sort | 메모리의 외부인 보조 기억 장치에서 정렬 |
정렬 장소
- 내부 정렬
내부 정렬은 정렬할 자료를 메인 메모리에 올려서 정렬하는데, 정렬 속도는 빠르지만 정렬할 자료의 양이 많다면 메인 메모리의 용량에 따라 제한된다. 그리고 내부 정렬은 사용하는 정렬 방식에 따라 나뉜다.
| 구분 | 종류 | 설명 |
| 비교식 | 교환 방식 | 키를 비교하여 정렬하는 방식 -> 선택 정렬, 버블 정렬, 퀵 정렬 |
| 삽입 방식 | 키를 비교하고 삽입하는 방식 -> 삽입 정렬, 셸 정렬 | |
| 병합 방식 | 키를 비교하고 병합하여 정렬하는 방식(2-way, n-way) | |
| 선택 방식 | 이진 트리를 사용하여 정렬하는 방식(히프 정렬, 트리 정렬) | |
| 분배식 | 분배 방식 | 키를 구성하는 값을 여러 개의 부분집합에 분배하여 정렬하는 방식(기수 정렬) |
- 외부 정렬
외부 정렬은 보조 기억 장치를 사용하기 때문에 내부 정렬보다 속도는 떨어지지만, 보조 기억 장치를 대용량으로 쓸 수 있어 내부 정렬로 처리할 수 없는 대용량 자료를 정렬할 수 있다. 이러한 정렬은 파일을 부분 파일로 분리하여 각각을 내부 정렬 방법으로 정렬하여 병합하는 2-way 병합, n-way 병합이 있다.
정렬의 종류
- 선택 정렬 (Selection Sort):
- 가장 작은(또는 큰) 원소를 찾아 첫 번째 원소와 교환하고, 그다음 작은(또는 큰) 원소를 찾아 두 번째 원소와 교환하는 과정을 반복하여 정렬하는 알고리즘.
- 시간 복잡도: O(n^2)
- 버블 정렬 (Bubble Sort):
- 인접한 두 원소를 비교하여 순서가 잘못되어 있으면 서로 교환하는 과정을 반복하여 정렬하는 알고리즘.
- 시간 복잡도: O(n^2)
- 퀵 정렬 (Quick Sort):
- 피벗(pivot)을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 분할하고, 분할된 부분 리스트에 대해 재귀적으로 정렬하는 알고리즘.
- 평균 시간 복잡도: O(n log n), 최악의 경우: O(n^2)
- 삽입 정렬 (Insertion Sort):
- 정렬된 부분 리스트와 비교하여 원소를 올바른 위치에 삽입하는 과정을 반복하여 정렬하는 알고리즘.
- 시간 복잡도: O(n^2)
- 셸 정렬 (Shell Sort):
- 일정한 간격으로 원소를 묶어 부분적으로 정렬하고, 간격을 줄여가며 최종적으로 정렬하는 알고리즘.
- 시간 복잡도: O(n log n) - O(n^2)
- 병합 정렬 (Merge Sort):
- 반으로 나눈 후 각 부분 리스트를 재귀적으로 정렬하고, 정렬된 부분 리스트를 병합하여 전체를 정렬하는 알고리즘.
- 시간 복잡도: O(n log n)
- 기수 정렬 (Radix Sort):
- 각 자릿수를 기준으로 정렬하는 알고리즘으로, 가장 낮은 자릿수부터 가장 높은 자릿수까지 차례로 정렬을 수행한다.
- 시간 복잡도: O(nk), 여기서 k는 숫자의 최대 자릿수
- 히프 정렬 (Heap Sort):
- 히프 자료구조를 사용하여 정렬하는 알고리즘. 주로 배열을 이진 히프로 구성하고 히프를 구성하면서 최대(또는 최소) 값을 추출하여 정렬한다.
- 시간 복잡도: O(n log n)
- 트리 정렬 (Tree Sort):
- 이진 검색 트리(Binary Search Tree)를 사용하여 정렬하는 알고리즘. 모든 원소를 트리에 삽입한 후 중위 순회를 수행하면 정렬된 결과를 얻을 수 있다.
- 시간 복잡도: O(n^2) - 평균적으로는 O(n log n)
각 정렬 알고리즘은 특정 상황에 더 효과적일 수 있으며, 선택해야 하는 경우에는 입력 데이터의 크기와 정렬 상태 등을 고려해하여 사용한다
그리고 시간 복잡도는 알고리즘이 입력 크기에 대해 얼마나 효율적으로 동작하는지를 나타내는 지표인데, 이를 이해하기 위해서 몇 가지 개념을 알아야 한다.
- O 표기법 (빅 오 표기법):
- O 표기법은 알고리즘의 성능을 "최악의 경우"에 대한 상한을 나타낸다.
- 예를 들어, O(n^2)은 입력 크기 n에 대해 최악의 경우에는 연산 횟수가 n^2에 비례한다는 것을 의미한다.
- 선형 시간과 비선형 시간:
- O(n)은 선형 시간을 나타내며, 입력 크기에 비례하여 선형적으로 증가한다.
- O(n^2), O(log n), O(n log n) 등은 비선형 시간을 나타내며, 입력 크기에 대한 다른 비율로 증가한다.
- 최선, 평균, 최악의 경우:
- 알고리즘의 성능은 최선의 경우, 평균적인 경우, 최악의 경우에 따라 다를 수 있다.
- 일반적으로 O 표기법은 최악의 경우를 나타낸다.
간단한 예시로 설명하면
- 선형 탐색 (Linear Search):
- 최악의 경우 시간 복잡도: O(n) - 입력 크기 n에 비례하여 순차적으로 모든 원소를 확인해야 할 수 있음.
- 이진 탐색 (Binary Search):
- 최악의 경우 시간 복잡도: O(log n) - 입력이 정렬되어 있어 이진 분할을 통해 검색하므로 로그 시간이 소요됨.
- 버블 정렬 (Bubble Sort):
- 최악의 경우 시간 복잡도: O(n^2) - 모든 원소를 서로 비교하며 정렬하기 때문에 n * (n-1) / 2 만큼의 비교와 교환이 필요.
- 병합 정렬 (Merge Sort):
- 최악의 경우 시간 복잡도: O(n log n) - 반으로 나누고 합치는 단계를 계속 반복하므로 로그 선형 시간이 소요됨.
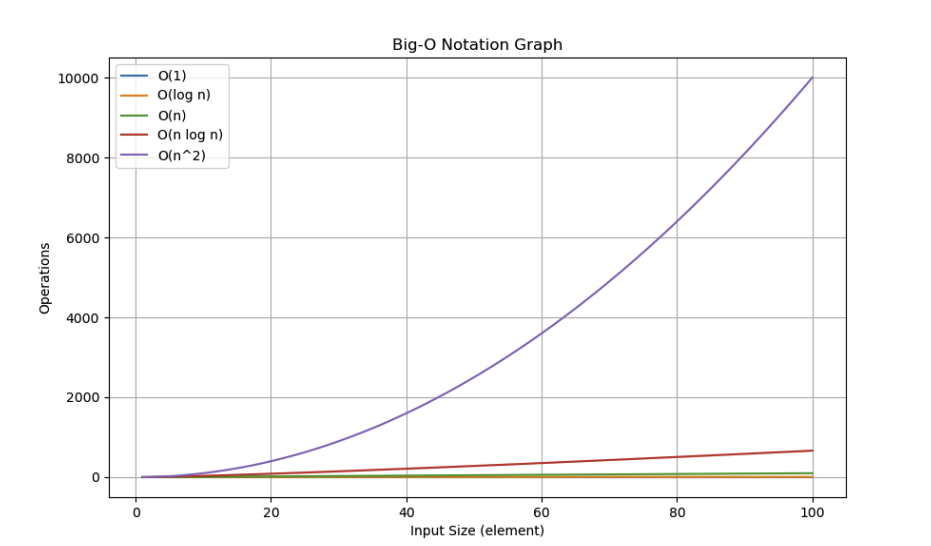
아! 이건 한번 파이선 코드로 작성해 보아 출력해 보았는데... 그냥 인터넷에 돌아다니는 사진을 보자..
즉, 시간 복잡도가 작을수록 알고리즘이 빠르게 동작하고, 특히 입력 크기가 증가할 때 성능이 어떻게 변하는지 예측할 수 있다.
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘] 정렬 3 - 삽입정렬, 셸 정렬 (0) | 2023.12.09 |
|---|---|
| [알고리즘] 정렬 2 - 선택 정렬, 버블 정렬, 퀵 정렬 (0) | 2023.12.09 |
| [알고리즘] 그래프 8 - 최단 경로(플로이드) (2) | 2023.12.08 |
| [알고리즘] 그래프 7 - 최단 경로(다익스트라) (1) | 2023.12.07 |
| [알고리즘] 그래프 6 - 신장 트리와 최소 비용 신장 트리 (0) | 2023.12.07 |