목차
크루스칼 알고리즘 2
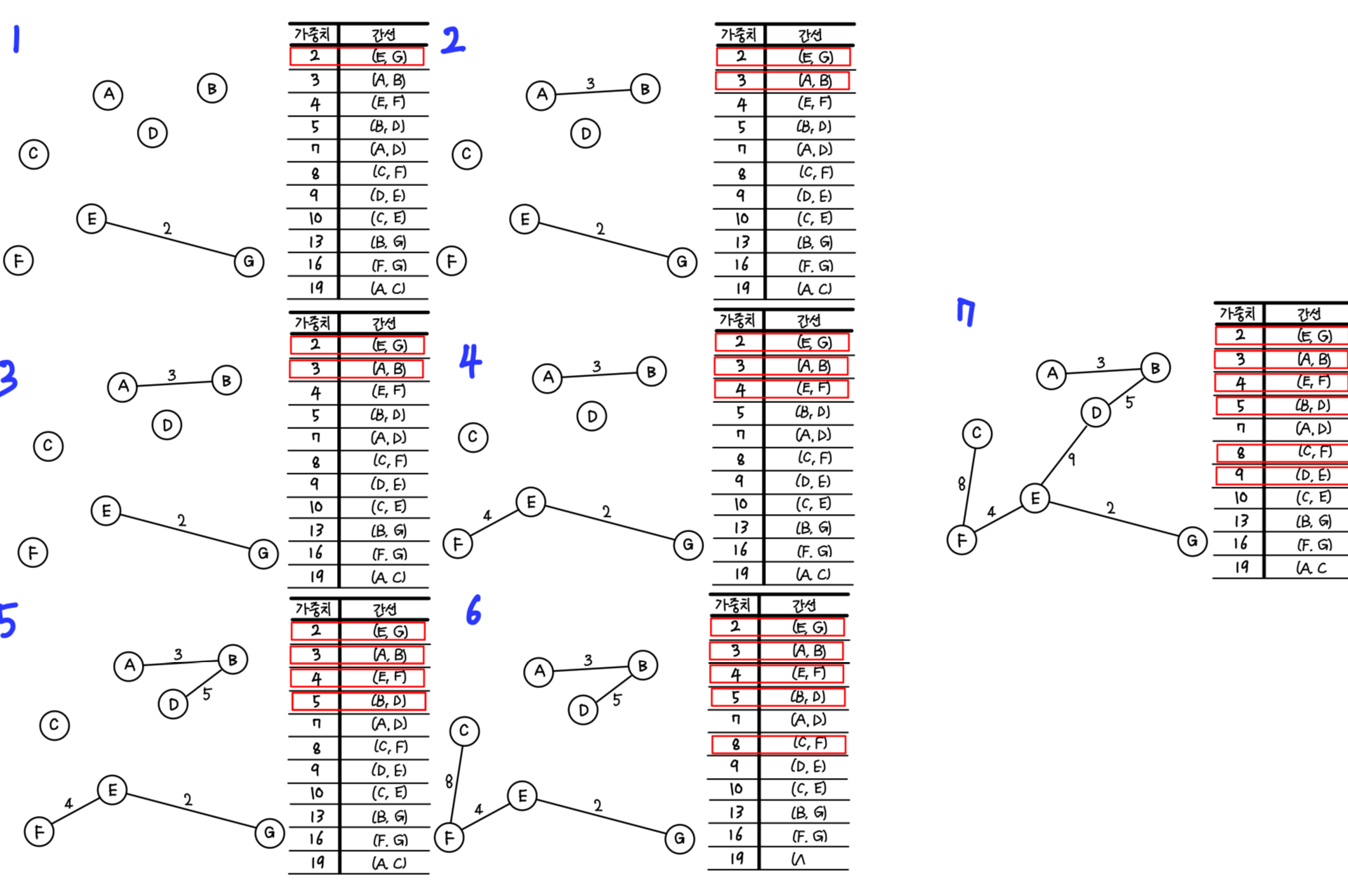
이 알고리즘은 가중치가 낮은 간선을 삽입하면서 최소 비용 신장 트리를 만들어가는 알고리즘이다.
크루스칼 알고리즘 2를 적용한 최소 비용 신장트리를 만들기 위해서는 밑에 4가지의 순서를 지키며 트리를 생성하면 되는데...
- 그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
- 그래프에서 가중치가 가장 낮은 간선을 삽입한다. 단, 이때 정점을 그래프에서 사이클을 형성하는 간선은 삽입할 수 없으므로 그다음으로 가중치가 낮은 간선을 삽입한다.
- 그래프에 간선이 n-1개 삽입될 때까지 2번 과정을 반복한다.
- 그래프에 간선이 n-1개가 되면최소 비용 신장 트리가 완성된다.
그렇다 이 순서를 읽어보면 크루스칼 알고리즘 1과 다르게 정점과 간선을 삽입하면서 최소 비용 신장 트리를 만들어가는 것이다.
그리고 이 크루스칼 알고리즘에 사용되는 자료구조에는 Union-Find가 사용이 된다.

#include <stdio.h>
#include <stdlib.h>
// 정점과 간선의 정보를 담는 구조체
typedef struct {
int src, dest, weight;
} Edge;
// 정점의 부모를 찾기 위한 Union-Find 자료 구조
typedef struct {
int *parent, *rank;
int num_nodes;
} UnionFind;
// Union-Find 자료 구조 초기화
UnionFind* createUnionFind(int num_nodes) {
UnionFind* uf = (UnionFind*)malloc(sizeof(UnionFind));
uf->parent = (int*)malloc(num_nodes * sizeof(int));
uf->rank = (int*)malloc(num_nodes * sizeof(int));
uf->num_nodes = num_nodes;
for (int i = 0; i < num_nodes; ++i) {
uf->parent[i] = i;
uf->rank[i] = 0;
}
return uf;
}
// 정점의 루트(부모)를 찾는 함수
int find(UnionFind* uf, int u) {
if (uf->parent[u] != u)
uf->parent[u] = find(uf, uf->parent[u]);
return uf->parent[u];
}
// 두 정점을 연결하는 함수 (Union 연산)
void unionSets(UnionFind* uf, int u, int v) {
int rootU = find(uf, u);
int rootV = find(uf, v);
if (rootU != rootV) {
if (uf->rank[rootU] < uf->rank[rootV])
uf->parent[rootU] = rootV;
else if (uf->rank[rootU] > uf->rank[rootV])
uf->parent[rootV] = rootU;
else {
uf->parent[rootU] = rootV;
uf->rank[rootV]++;
}
}
}
// 간선을 가중치에 따라 오름차순으로 정렬하는 비교 함수
int compareEdges(const void* a, const void* b) {
return ((Edge*)a)->weight - ((Edge*)b)->weight;
}
// 크루스칼 알고리즘 함수
void kruskal(Edge edges[], int num_edges, int num_nodes) {
// 간선을 가중치에 따라 오름차순으로 정렬
qsort(edges, num_edges, sizeof(Edge), compareEdges);
// Union-Find 자료 구조 초기화
UnionFind* uf = createUnionFind(num_nodes);
printf("Minimum Spanning Tree Edges:\n");
// 간선을 하나씩 확인하면서 사이클이 형성되지 않으면 선택
for (int i = 0; i < num_edges; ++i) {
int src = edges[i].src;
int dest = edges[i].dest;
if (find(uf, src) != find(uf, dest)) {
printf("(%d, %d) - Weight: %d\n", src, dest, edges[i].weight);
unionSets(uf, src, dest);
}
}
free(uf->parent);
free(uf->rank);
free(uf);
}
int main() {
// 주어진 Edge 배열
Edge edges[] = {
{0, 2, 17}, {5, 6, 14}, {1, 6, 12}, {2, 4, 10}, {3, 4, 9},
{2, 5, 8}, {0, 3, 6}, {1, 3, 5}, {4, 5, 4}, {0, 1, 3}, {4, 6, 2}
};
// 정점의 개수와 간선의 개수 계산
int num_nodes = 7;
int num_edges = sizeof(edges) / sizeof(edges[0]);
// 크루스칼 알고리즘 호출
kruskal(edges, num_edges, num_nodes);
return 0;
}크루스칼 알고리즘 1에 비하면 엄청 쉽다.
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 8 - 최단 경로(플로이드) (2) | 2023.12.08 |
|---|---|
| [알고리즘] 그래프 7 - 최단 경로(다익스트라) (1) | 2023.12.07 |
| [알고리즘] 그래프 5 - 신장 트리와 최소 비용 신장 트리 (1) | 2023.12.07 |
| [알고리즘] 그래프 4 - 그래프의 순회(너비 우선 탐색 BFS) (1) | 2023.12.05 |
| [알고리즘] 그래프 3 - 그래프의 순회(깊이 우선 탐색 DFS) (0) | 2023.12.05 |