최단 경로
최단 경로는 신장 트리가 아닌 가중치 그래프, 즉 네트워크에서 정점 u와 정점 v를 연결하는 경로 중에서 가중치의 합이 최소인 경로이다.
예를 들어 지하철 노선 어플을 보면 내가 원하는 출발지에서 목적지까지의 최단 경로를 구하는 어플, 그리고 내비게이션이 있다.
이러한 최단 경로를 구하는 가중치 그래프에서는 가중치 인접 행렬 Weight Adjacent Matrix를 사용하는데, 이 가중치 인접 행렬은 2차원 배열이며, 두 정점 사이에 간선이 없으면 0이 아니라 무한∽이라는 값이 저장되어 있다고 가정하고 사용한다.

그렇게 최단 경로를 찾는 방법에는 하나의 시작 정점에서 다른 정점까지의 최단 경로를 구하는 다익스트라 Dijkstra 최단 경로 알고리즘과 모든 정점에서 다른 모든 정점까지의 최단 경로를 구하는 플로이드 Floyd최단 경로 알고리즘이 있다.
다익스트라 최단 경로 알고리즘
다익스트라(Dijkstra) 최단 경로 알고리즘은 주어진 그래프에서 특정 출발점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘 중 하나로 가중 그래프에서 사용되며, 간선의 가중치가 음수일 때는 사용할 수 없다.
다익스트라의 기본 원리는 특정 시작 정점 v에서 가장 가까운 정점을 선택하여 추가하면서 추가된 새로운 정점에 의해 단축되는 경로가 있다면, 경로 간의 거리를 다시 수정하여 시작 정점에서 모든 정점에 대한 최단 경로는 구한다.
1.우선 초기에 A를 시작으로 하였을 때 A에서의 거리 값은 B(10), C(5), D(무한), E(무한)이다. 이를 경로 배열에 넣고 집합 배열에는 A를 방문하였으므로 A인덱스에 T를 넣는다.

2.그다음 경로 배열에서 가중치 값이 가장 작은 값을 가지는 C로 이동하여 C에서 아직 방문하지 않은 B,D,E의 거리를 다시 계산하여 경로 배열에 집어 넣는다.
실제로 방문하는 정점 : A -> C -> B / A -> C -> D / A -> C -> E
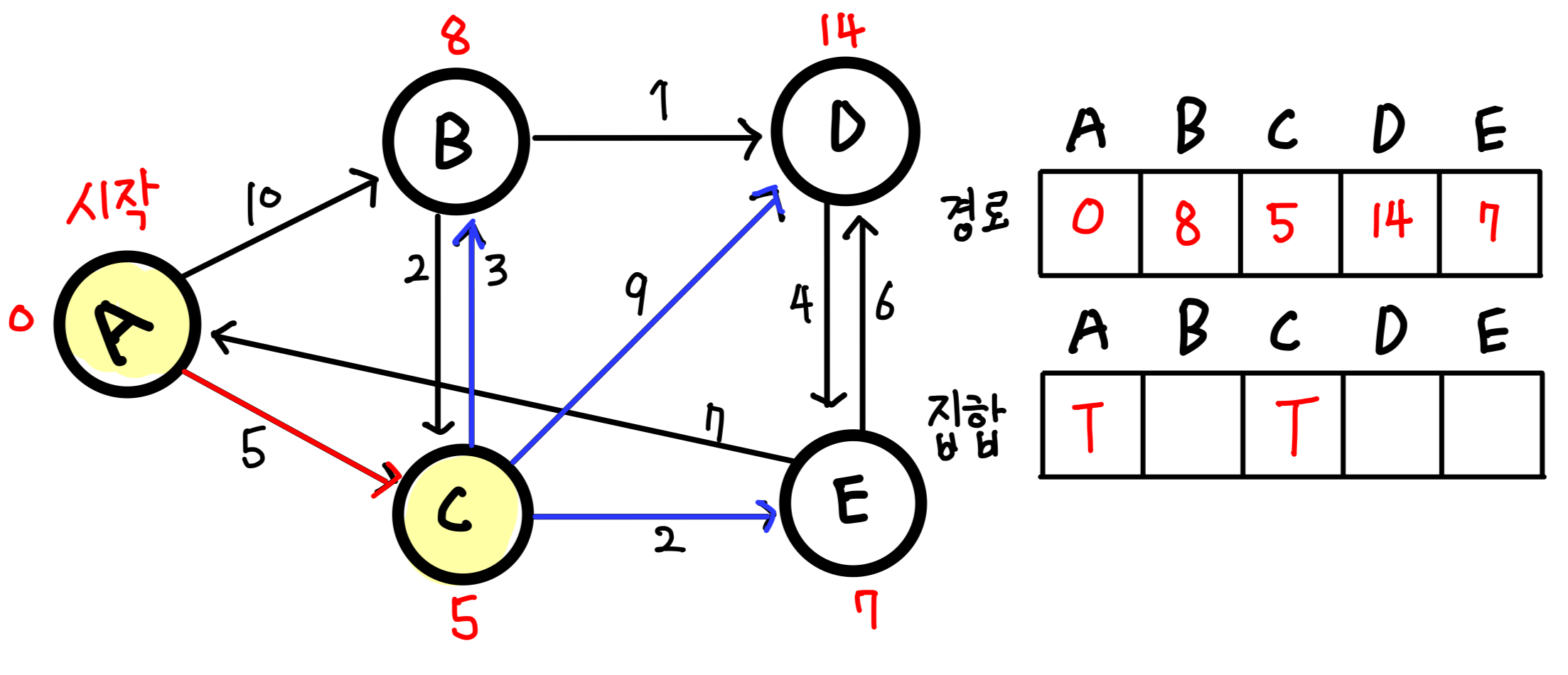
3.그 다음 경로 배열에서 가중치 값이 가장 작은 값을 가지는 E로 이동(방문하였던 A,C는 제외)하여서 E에서 아직 방문하지 않은 B와 D까지의 거리를 다시 계산하여 경로 배열에 집어 넣는다. E에서 D로 가는 경로의 길이는 줄었지만 E에서 B로 가는 경로의 길이는 오히려 길어지므로 배열에 반영하지 않는다.
실제 방문하는 정점 : A -> C -> E -> D / A -> C -> E -> A -> B - > D (오히려 늘어난다. B를 방문해도 마찬가지.)

4.그 다음 경로 배열에서 가중치 값이 가장 작은 값을 가지는 B로 이동(방문하였던A,C,E는 제외)하여서 거리를 계산해본다.
실제 방문하는 정점 : A -> C -> B -> D , 다른 경로도 많지만 거리가 증가함.

5. 그 다음 로 배열에서 가중치 값이 가장 작은 값을 가지는 D로 이동하면 모든 정점이 집합에 추가되었으므로 최단 경로가 완성된다.
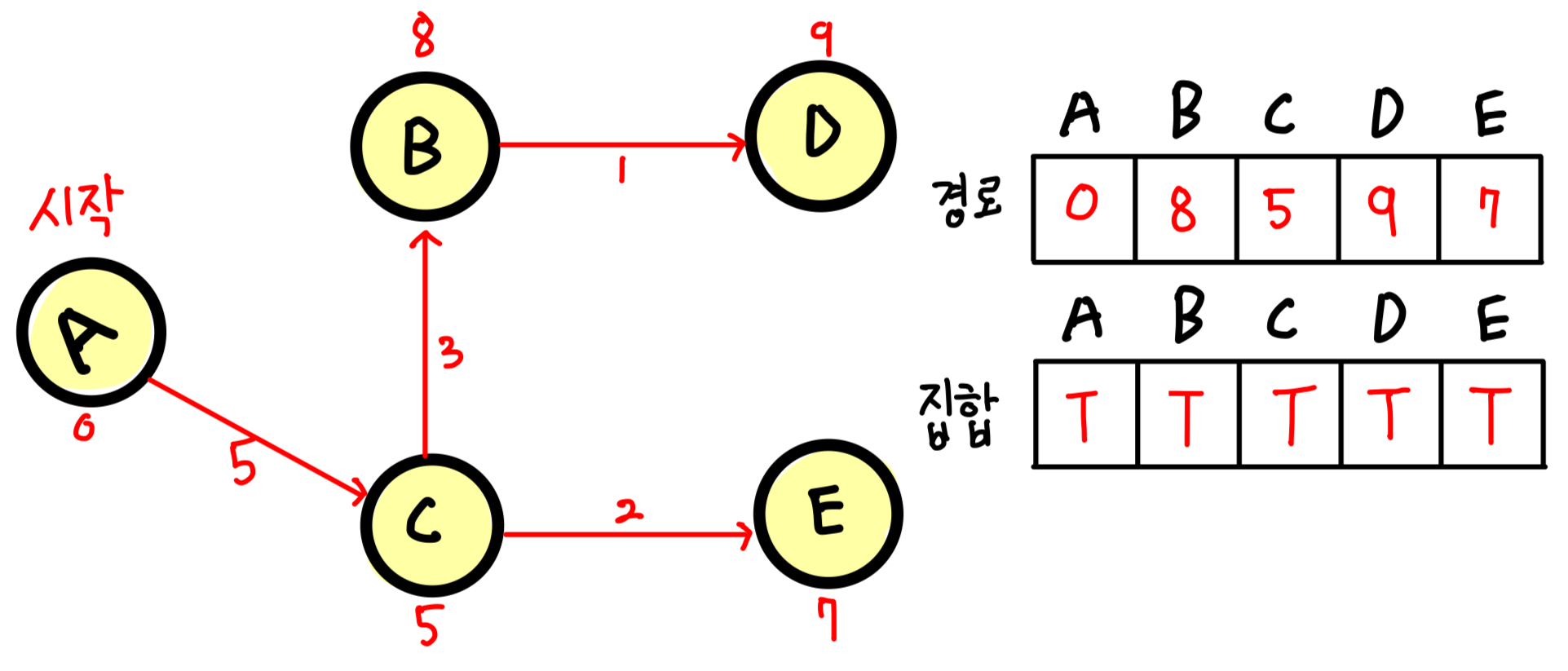
혹시 이해가 안된다면 코드를 필독하면 좋다. 왜냐하면 경로를 찾을 때 어떻게 방문해야하는지 헷갈리기 때문이다.
이미 방문했던 정점은 다시는 방문하지 않는다. 즉 방문하지 않은 정점들만 방문한다. 이게 특징이다.
// 헤더 파일 및 상수 정의
#pragma once
#include <stdio.h>
#include <limits.h>
#define TRUE 1
#define FALSE 0
#define INF 10000 // 무한대 값
#define MAX_VERTICES 5 // 그래프의 정점 개수
// 전역 변수 선언
int distance[MAX_VERTICES]; // 시작 정점으로부터의 최단 경로 길이 저장
int S[MAX_VERTICES]; // 정점의 집합 S
// 그래프 G11의 가중치 인접행렬
int weight[MAX_VERTICES][MAX_VERTICES] = {
{ 0, 10, 5, INF, INF },
{ INF, 0, 2, 1, INF },
{ INF, 3, 0, 9, 2 },
{ INF, INF, INF, 0, 4 },
{ 7, INF, INF, 6, 0 }
};
// 최소 거리를 갖는 다음 정점을 찾는 연산
int nextVertex(int n) {
int i, min, minPos;
min = INF;
minPos = -1;
// 각 정점에 대해 최소 거리를 찾음
for (i = 0; i < n; i++)
// 최단 경로이면서 아직 집합 S에 속하지 않은 경우
if ((distance[i] < min) && !S[i]) {
min = distance[i];
minPos = i;
}
return minPos;
}
// 최단 경로 구하는 과정을 출력하는 연산
int printStep(int step) {
int i;
printf("\n %3d 단계 : S={", step);
// 현재까지 선택된 정점들을 출력
for (i = 0; i < MAX_VERTICES; i++)
if (S[i] == TRUE)
printf("%3c", i + 65);
// 출력 포맷 조정
if (step < 1) printf(" } \t\t\t");
else if (step < 4) printf(" } \t\t");
else printf(" } \t");
printf(" distance :[ ");
// 각 정점까지의 최단 거리 출력
for (i = 0; i < MAX_VERTICES; i++)
if (distance[i] == INF) printf("%4c", '*');
else printf("%4d", distance[i]);
printf("%4c", ']');
return ++step;
}
// 다익스트라 구현
void Dijkstra_shortestPath(int start, int n) {
int i, u, w, step = 0;
// 초기화
for (i = 0; i < n; i++) {
distance[i] = weight[start][i];
S[i] = FALSE;
}
S[start] = TRUE; // 시작 정점을 집합 S에 추가
distance[start] = 0; // 시작 정점의 최단경로를 0으로 설정
step = printStep(0); // 0단계 상태를 출력
// n-1번 반복 (각 정점에 대한 처리)
for (i = 0; i < n - 1; i++) {
u = nextVertex(n); // 최단 경로를 만드는 다음 정점 u 찾기
S[u] = TRUE; // 정점 u를 집합 S에 추가
// 집합 S에 속하지 않은 정점 중에서
for (w = 0; w < n; w++)
if (!S[w])
// 현재까지의 최단 경로보다 더 짧은 경로가 있으면 업데이트
if (distance[u] + weight[u][w] < distance[w])
distance[w] = distance[u] + weight[u][w]; // 경로 길이 수정
step = printStep(step); // 현재 단계 출력
}
}
// 메인 함수
int main(void) {
int i, j;
// 가중치 인접 행렬 출력
printf("\n ********** 가중치 인접 행렬 **********\n\n");
for (i = 0; i < MAX_VERTICES; i++) {
for (j = 0; j < MAX_VERTICES; j++) {
// 무한대 값인 경우 '*' 출력, 아니면 가중치 값 출력
if (weight[i][j] == INF)
printf("%4c", '*');
else printf("%4d", weight[i][j]);
}
printf("\n\n");
}
// 다익스트라 알고리즘 수행
printf("\n ********* 다익스트라 최단 경로 구하기 **********\n");
Dijkstra_shortestP
********** 가중치 인접 행렬1 **********
0 10 5 * *
* 0 2 1 *
* 3 0 9 2
* * * 0 4
7 * * 6 0
********* 다익스트라 최단 경로 구하기1 **********
0 단계 : S={ A } distance :[ 0 10 5 * * ]
1 단계 : S={ A C } distance :[ 0 8 5 14 7 ]
2 단계 : S={ A C E } distance :[ 0 8 5 13 7 ]
3 단계 : S={ A B C E } distance :[ 0 8 5 9 7 ]
4 단계 : S={ A B C D E } distance :[ 0 8 5 9 7 ]'알고리즘' 카테고리의 다른 글
| [알고리즘] 정렬 1 (1) | 2023.12.08 |
|---|---|
| [알고리즘] 그래프 8 - 최단 경로(플로이드) (2) | 2023.12.08 |
| [알고리즘] 그래프 6 - 신장 트리와 최소 비용 신장 트리 (0) | 2023.12.07 |
| [알고리즘] 그래프 5 - 신장 트리와 최소 비용 신장 트리 (1) | 2023.12.07 |
| [알고리즘] 그래프 4 - 그래프의 순회(너비 우선 탐색 BFS) (1) | 2023.12.05 |