[알고리즘] 트리6 - 히프 트리(Heap)

알고리즘

[알고리즘] 트리6 - 히프 트리(Heap)

sundori 2023. 11. 20. 15:24

ㅊ2023.11.14 - [알고리즘] - [알고리즘] 트리 5 - 균형 이진 탐색 트리(AVL)

[알고리즘] 트리5 - 균형 이진 탐색 트리(AVL)

목차 2023.11.13 - [알고리즘] - [알고리즘] 트리 4 - 이진 탐색 트리 [알고리즘] 트리4 - 이진 탐색 트리 이진 탐색 트리 이진트리는 트리를 효율적으로 구현하고 관리하기 위해서 일정한 조건으로 정

sun-dori.tistory.com

히프

히프는 완전 이진 트리에 있는 노드 중에서 키값이 가장 큰 노드나 키잡이 가장 작은 노드를 찾을 때 필요한 자료구조이다.

키값이 가장 큰 노드를 찾기 위한 히프를 최대 히프(Max Heap), 키값이 가장 작은 노드를 찾기 위한 히프를 최소 히프(Min Heap)라 한다.

히프의 개념

최대 히프
최대 히프는 부모 노드의 키값이 자식 노드의 키값보다 항상 크거나 같은 크기의 관계로 (부모 노드의 키값 ≥ 자식 노드의 키값)의 관계를 가지는 완전 이진 트리이여서 최대 히프에서 키값이 가장 큰 노드는 루트 노드이다.
최소 히프
최소 히프는 부모 노드의 키값이 자식 노드의 키값보다 항상 작거나 같은 크기를 가지는 관계로 (부모 노드의 키값 ≤ 자식 노드의 키값)의 관계를 가지는 완전 이진 트리이며 키값이 가장 작은 노드는 루트 노드가 된다.

히프의 삽입 연산

최대 히프에서의 삽입 연산은 완전 이진 트리의 형태의 조건을 만족해야 하기에 현재의 마지막 노드의 다음 자리를 확장하여 자리를 만들고, 삽입할 원소를 임시로 저장한 뒤에 키값의 관계가 최대 히프가 되도록 재구성하기 위해 삽입한 원소의 키값과 현재 임시 위치에서의 부모 노드의 키값을 비교한다.

최소 히프에서의 삽입 연산은 완전 이진 트리의 형태를 유지하면서, 현재의 마지막 노드의 다음 자리를 확장하여 자리를 만들고, 삽입할 원소를 임시로 저장한 뒤에 키값의 관계가 최소 히프가 되도록 재구성한다.

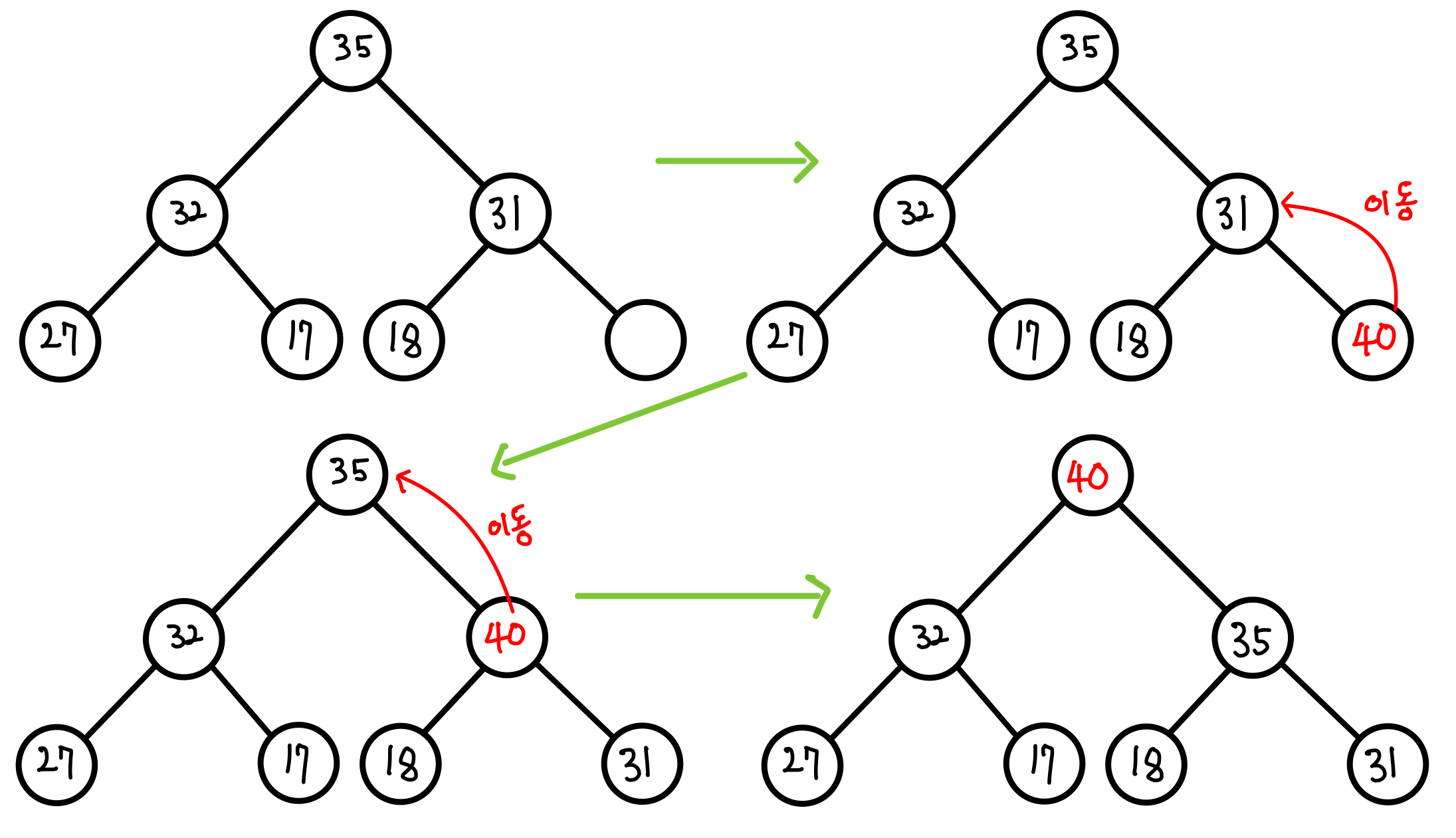
최대 히프의 삽입 연산
1.원소 삽입 : 새로운 원소를 히프의 마지막 위치에 추가한다.
2. 부모 노드와 비교 : 삽입된 원소를 현재 위치에서 부모 노드의 위치와 비교한다.
3. 조건 비교 및 교환 : 만약 삽입된 원소의 키값이 부모 노드의 키값보다 크다면 두 노드의 위치를 교환한다.
4. 재귀적 호출 : 교환된 위치에서 다시 부모 노드와 비교하여 이 과정을 반복하는데 최종적으로 (부모 노드의 키값 ≥ 자식 노드의 키값)
의 조건을 충족할 때까지 반복한다.

최소 히프의 삽입 연산
1. 원소 삽입 : 새로운 원소를 히프의 마지막 위치에 추가한다.
2. 부모 노드와 비교 : 삽입된 원소를 현재 위치에서 부모 노드의 위치와 비교한다.
3. 조건 비교 및 교환 : 만약 삽입된 원소의 키값이 부모 노드의 키값보다 작다면 두 노드의 위치를 교환한다.
4. 재귀적 호출 : 교환된 위치에서 다시 부모 노드와 비교하여 이 과정을 반복하는데 최종적으로 (부모 노드의 키값 ≥ 자식 노드의 키값)
의 조건을 충족할 때까지 반복한다.

히프의 삭제 연산

삭제는 루트 노드를 삭제하는데 이후 가장 마지막 노드를 루트 노드 자리에 대체한 뒤 재구조화 과정을 수행한다. (우선순위 큐에서도 가장 우선순위가 높은 루트 노드를 주로 삭제한다.) 즉, 히프에서의 삭제 연산은 언제나 루트 노드에 있는 원소를 삭제하는데 최대 히프에서는 키값이 가장 큰 값이 삭제되는 것이고 최소 히프에서는 키값이 가장 작은 원소가 삭제되는 것이며, 삭제 연산 후 완전 이진트리의 형태와 키값에 대한 히프의 조건이 충족되어야 한다.

최대 히프의 삭제 연산
1. 루트 노드 제거 : 최대 히프에서는 루트 노드가 항상 최댓값이기에 루트 노드를 제거한다.
2. 마지막 노드 이동 : 히프의 마지막 노드를 루트 노드로 이동시킨다.
3. 자식 노드와의 비교 : 자식 노드 중 더 큰 값과 비교하여 서로 위치를 교환한다.
4. 재귀적 호출 : 교환된 위치에서 다시 자식 노드와 비교하며 조건을 충족할 때까지 반복한다.

최소 히프의 삭제 연산
1. 루트 노드 제거 : 최소 히프에서는 루트 노드가 항상 최솟값이기에 루트 노드를 제거한다.
2. 마지막 노드 이동 : 히프의 마지막 노드를 루트 노드로 이동시킨다.
3. 자식 노드와의 비교 : 자식 노드 중 더 작은 값과 비교하여 서로 위치를 교환한다.
4. 재귀적 호출 : 교환된 위치에서 다시 자식 노드와 비교하며 조건을 충족할 때까지 반복한다.

히프의 구현

1차원 배열의 순차 자료구조 방식으로 구현하여 인덱스 관계를 사용하는데 그 이유는 부모 노드를 찾기 쉬워서이다.

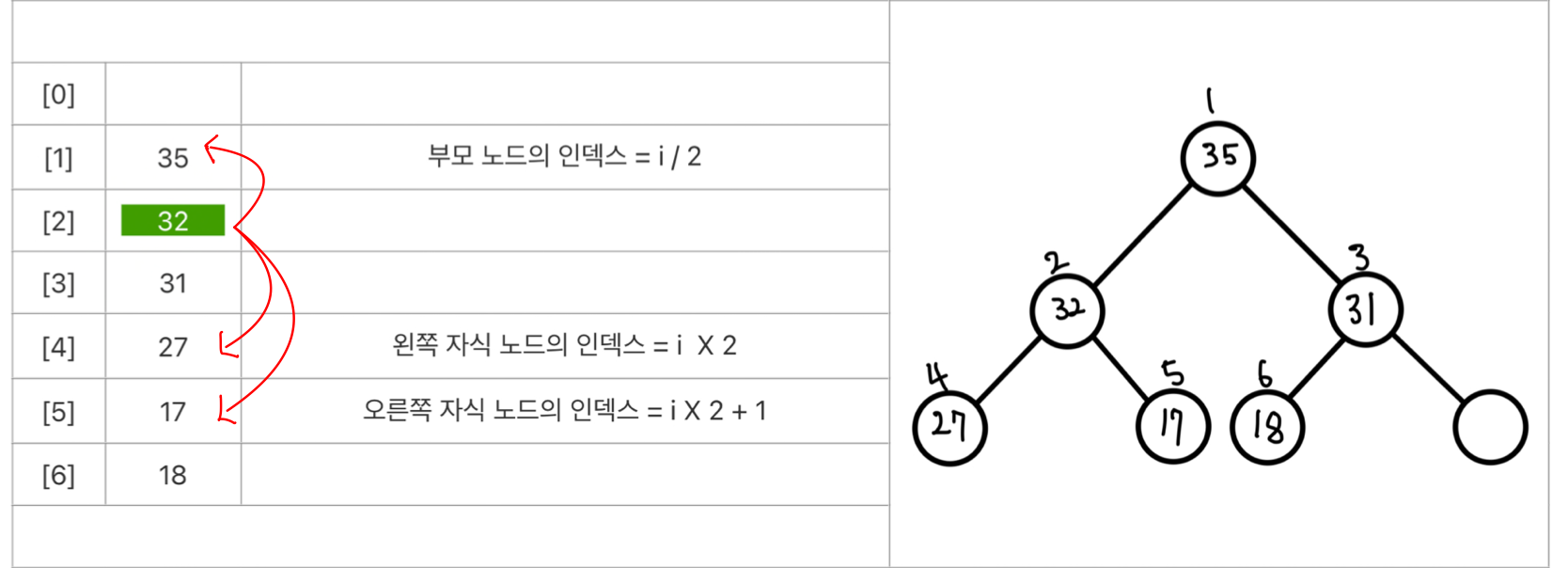
최대 히프

#include <stdio.h>
#include <stdlib.h>

#define MAX_ELEMENT 100

// 히프에 대한 1차원 배열과 히프 원소의 개수를 구조체로 묶어서 선언.
typedef struct {
    int heap[MAX_ELEMENT];
    int heap_size;
} heapType;

// 공백 히프를 생성하는 연산
heapType* createHeap() {
    heapType* h = (heapType*)malloc(sizeof(heapType));
    h->heap_size = 0;
    return h;
} 
 
// 히프에 item을 삽입하는 연산
void insertHeap(heapType* h, int item) {
    int i; 
    h->heap_size = h->heap_size + 1;
    i = h->heap_size; // i는 삽입될 위치를 나타내는 변수로 초기화.

    // 삽입된 원소를 부모 노드들과 비교하여 히프 속성을 만족시키도록 조정.
    while ((i != 1) && (item > h->heap[i / 2])) {
        h->heap[i] = h->heap[i / 2];
        i /= 2;
    }
    h->heap[i] = item; // 새로운 원소를 히프에 삽입한다.
}

// 최대 히프의 루트를 삭제하여 반환하는 연산
int deleteHeap(heapType* h) {
    int parent, child;
    int item, temp;
    item = h->heap[1]; // 삭제될 루트 원소를 저장.
    temp = h->heap[h->heap_size]; // 히프의 마지막 원소를 임시로 저장.
    h->heap_size = h->heap_size - 1; // 히프 크기를 감소.
    parent = 1;
    child = 2;

    // 마지막 원소를 루트로 올리면서 히프 속성을 만족시키도록 조정.
    while (child <= h->heap_size) {
        // 현재 노드의 자식 중 큰 값을 찾는다.
        if ((child < h->heap_size) && (h->heap[child] < h->heap[child + 1]))
            child++;
        
        // 임시로 저장한 마지막 원소가 자식보다 크거나 같으면 조정을 종료.
        if (temp >= h->heap[child]) break;
        else {
            // 자식이 더 크면 부모와 자리를 교환하고 계속 조정.
            h->heap[parent] = h->heap[child];
            parent = child;
            child = child * 2;
        }
    }
    h->heap[parent] = temp; // 마지막 원소를 최종적으로 삽입.
    return item; // 삭제된 루트 원소를 반환.
}

// 1차원 배열 히프의 내용을 출력하는 연산
void printHeap(heapType* h) {
    int i;
    printf("Heap : ");
    for (i = 1; i <= h->heap_size; i++)
        printf("[%d] ", h->heap[i]);
}

int main(void) {
    int i, n, item;
    heapType* heap = createHeap();

    // 히프에 원소를 삽입.
    insertHeap(heap, 15);
    insertHeap(heap, 18);
    insertHeap(heap, 21);
    insertHeap(heap, 31);
    insertHeap(heap, 17);
    insertHeap(heap, 20);
    insertHeap(heap, 32);
    insertHeap(heap, 27);
    insertHeap(heap, 35);

    // 히프의 내용을 출력.
    printHeap(heap);

    n = heap->heap_size;
    for (i = 1; i <= n; i++) {
        // 히프에서 원소를 삭제하면서 출력.
        item = deleteHeap(heap);
        printf("\n delete : [%d] ", item);
    }

    getchar();
    return 0;
}
--------------------------------
Heap : [35] [32] [31] [27] [17] [18] [20] [15] [21] 
 delete : [35] 
 delete : [32] 
 delete : [31] 
 delete : [27] 
 delete : [21] 
 delete : [20] 
 delete : [18] 
 delete : [17] 
 delete : [15]

최소 히프

#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 100

// 히프에 대한 1차원 배열과 히프 원소의 개수를 구조체로 묶어서 선언.
typedef struct {
    int heap[MAX_ELEMENT];
    int heap_size;
} heapType;

// 공백 히프를 생성하는 연산
heapType* createHeap() {
    heapType* h = (heapType*)malloc(sizeof(heapType));
    h->heap_size = 0;
    return h;
}

// 히프에 item을 삽입하는 연산
void insertHeap(heapType* h, int item) {
    int i;
    h->heap_size = h->heap_size + 1;
    i = h->heap_size;
    // 삽입된 원소를 부모 노드들과 비교하여 히프 속성을 만족시키도록 조정.
    while ((i != 1) && (item < h->heap[i / 2])) {
        h->heap[i] = h->heap[i / 2];
        i /= 2;
    }
    h->heap[i] = item;
}

// 최소 히프의 루트를 삭제하여 반환하는 연산
int deleteHeap(heapType* h) {
    int parent, child;
    int item, temp;
    item = h->heap[1];
    temp = h->heap[h->heap_size];
    h->heap_size = h->heap_size - 1;
    parent = 1;
    child = 2;

    // 마지막 원소를 루트로 올리면서 히프 속성을 만족시키도록 조정.
    while (child <= h->heap_size) {
        // 현재 노드의 자식 중 작은 값을 찾는다.
        if ((child < h->heap_size) && (h->heap[child] > h->heap[child + 1]))
            child++;

        // 임시로 저장한 마지막 원소가 자식보다 작거나 같으면 조정을 종료.
        if (temp <= h->heap[child]) break;
        else {
            // 자식이 더 작으면 부모와 자리를 교환하고 계속 조정.
            h->heap[parent] = h->heap[child];
            parent = child;
            child = child * 2;
        }
    }
    h->heap[parent] = temp; // 마지막 원소를 최종적으로 삽입.
    return item; // 삭제된 루트 원소를 반환.
}

// 1차원 배열 히프의 내용을 출력하는 연산
void printHeap(heapType* h) {
    int i;
    printf("Heap : ");
    for (i = 1; i <= h->heap_size; i++)
        printf("[%d] ", h->heap[i]);
}

int main() {
    int i, n, item;
    heapType* heap = createHeap();

    // 히프에 원소를 삽입.
    insertHeap(heap, 15);
    insertHeap(heap, 18);
    insertHeap(heap, 21);
    insertHeap(heap, 31);
    insertHeap(heap, 17);
    insertHeap(heap, 20);
    insertHeap(heap, 32);
    insertHeap(heap, 27);
    insertHeap(heap, 35);

    // 히프의 내용을 출력.
    printHeap(heap);

    n = heap->heap_size;
    for (i = 1; i <= n; i++) {
        // 히프에서 원소를 삭제하면서 출력.
        item = deleteHeap(heap);
        printf("\n delete : [%d] ", item);
    }

    // 삭제 후 히프의 내용을 출력.
    printHeap(heap);

    getchar();
    return 0;
}
-----------------------------------
Heap : [15] [17] [20] [27] [18] [21] [32] [31] [35] 
 delete : [15] 
 delete : [17] 
 delete : [18] 
 delete : [20] 
 delete : [21] 
 delete : [27] 
 delete : [31] 
 delete : [32] 
 delete : [35]

728x90

'알고리즘' 카테고리의 다른 글

[알고리즘] 그래프 2 - 그래프의 구현(인접 행렬) (0)	2023.12.05
[알고리즘] 그래프 1 - 그래프의 개념 (1)	2023.12.05
[알고리즘] 트리5 - 균형 이진 탐색 트리(AVL) (0)	2023.11.14
[알고리즘] 트리4 - 이진 탐색 트리 (0)	2023.11.13
[알고리즘] 트리3 - 스레드 이진 트리 (1)	2023.11.13

현재글[알고리즘] 트리6 - 히프 트리(Heap)

낭만을 찾아서 개발자의 길에 오르기 시작하다.

알고리즘, 극동대학교, 자료구조, C/C++, 프로그래머스, CodeVisionAVR, 스위치를 이용한 LED 컨트롤, Lv.0, java, 극동대학교 AI컴퓨터, LV0, 추상 클래스, Atmega128보드, 자바, 트리, IntStream, 극동대, 태양계, 임베디드시스템, 코딩 기초 트레이닝,

Today :
Yesterday :

sundori DevStory

[알고리즘] 트리6 - 히프 트리(Heap)