목차
스레드 이진트리(Thread Binary Tree)
이전 글 이진 트리의 순회에서는 부모 노드와 자식 노드의 이진트리 기본 구조에서 각 레벨에서 순환적으로 반복되어 전체 트리가 구성되는 구조이다 보니 각 노드에서의 순회 연산을 재귀호출을 이용하여 순환적으로 반복하여 전체 트리에 대한 순회를 처리하였다.
이러한 방식은 함수 구현을 함에 있어서 간단하지만, 수행의 성능 측면에서는 시스템적으로 스택을 사용하여 호출과 복귀를 관리해야하고 이진트리의 하위 레벨로 내려갈수록 재귀호출의 깊이가 깊어지므로(스택에 쌓이는 양이 많아짐) 매우 비효율적일 수 있다.
따라서 이러한 문제점들을 생각하여 재귀호출이 없어도 순회가 가능토록한 것이 스레드 이진트리이다.
스레드 이진트리의 특징
- 스레드 (Thread)
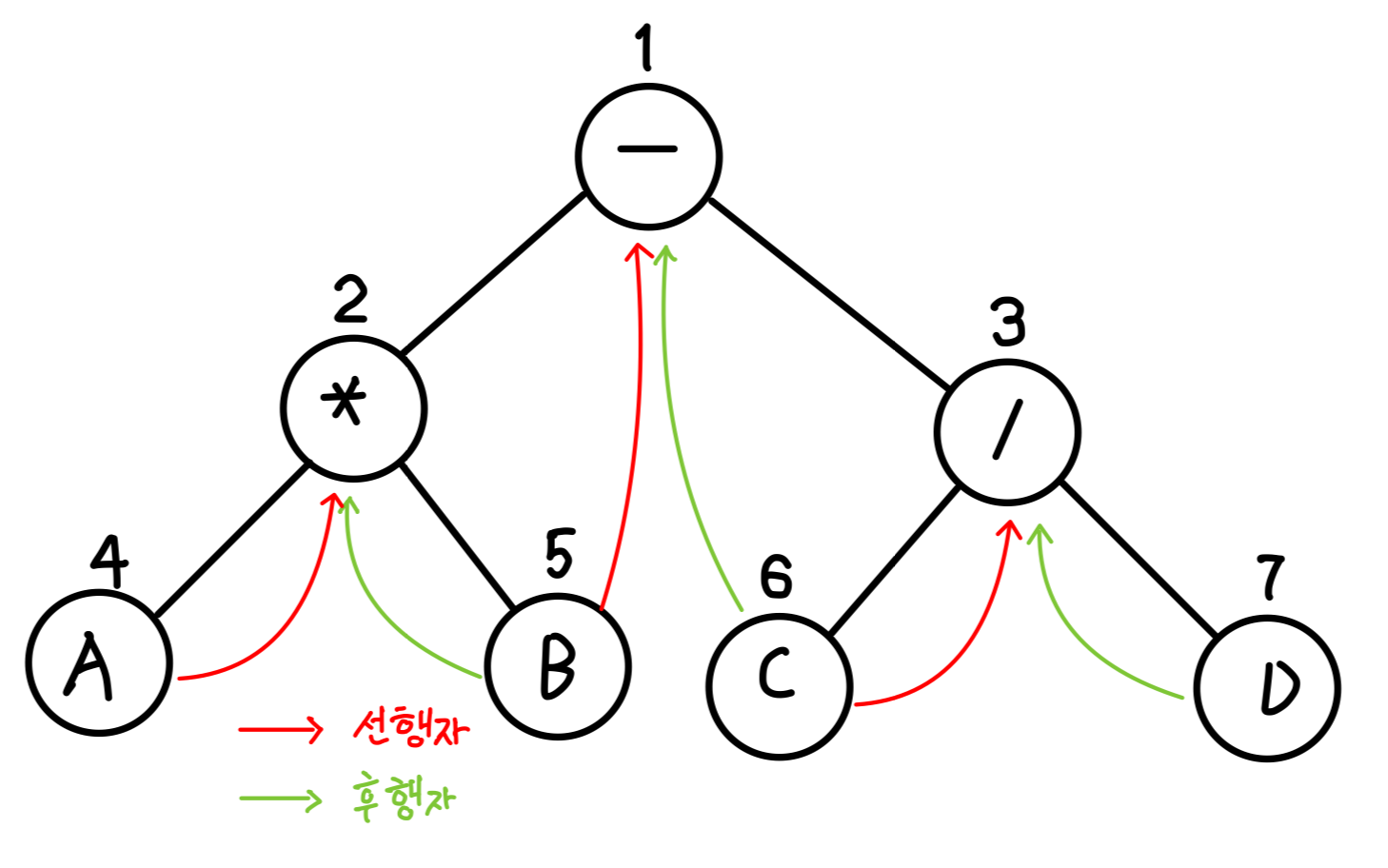
스레드 이진 트리는 자식 노드가 없는 경우에 링크 필드를 널 포인터 대신 순회 순서상의 다른 노드를 가르키도록 함. - 선행자 (Predecesssor)
스레드 이진 트리에서 이진 트리의 순회 경로에 다라 현재 노드 직전에 처리한 노드, 즉 선행자에 대한 포인터를 현재 왼쪽 노드의 왼쪽 널 대신에 저장. - 후행자 (Successor)
현재 노드 직후에 처리할 노드, 즉 후행자에 대한 포인터를 현재 노드의 오른쪽 널 링크 대신에 저장.
// 스레드 이진 트리 노드 구조체 정의
struct treeThNode {
char data; // 노드의 데이터 (문자)
struct treeThNode* left; // 왼쪽 서브 트리 링크
struct treeThNode* right; // 오른쪽 서브 트리 링크
int isThreadLeft; // 본 코드에서는 사용안함.
int isThreadRight; // 오른쪽 노드가 후행자인지 여부를 나타내는 플래그 (1이면 후행자)
};- isThread 필드
링크 필드가 자식 노드에 대한 포인터인지 아니면 자식 노드 대신 스레드가 저장되어 있는지 구별하기 위한 태그 필드. - isThreadLeft 선행자
true이면 left링크 필드는 선행자를 가리키는 스레드이고, false이라면 링크 필드는 왼쪽 자식 노드에 대한 포인터. - isThreadRight 후행자
true이면 right 링크 필드는 후속자를 가리키는 스레드이고, false이라면 링크 필드는 오른쪽 자식 노드에 대한 포인터.
//
// ex7_3.c
// Algorithm
//
// Created by 권xx on 2023/09/18.
//
#include <stdio.h>
#include <stdlib.h>
// 스레드 이진 트리 노드 구조체 정의
struct treeThNode {
char data; // 노드의 데이터 (문자)
struct treeThNode* left; // 왼쪽 서브 트리 링크
struct treeThNode* right; // 오른쪽 서브 트리 링크
int isThreadRight; // 오른쪽 노드가 후행자인지 여부를 나타내는 플래그 (1이면 후행자)
};
// data를 루트 노드로 하여 왼쪽 서브 트리와 오른쪽 서브 트리를 연결하는 연산
struct treeThNode* makeRootThNode(char data, struct treeThNode* leftNode, struct treeThNode* rightNode, int isThreadRight) {
struct treeThNode* root = (struct treeThNode*)malloc(sizeof(struct treeThNode));
(*root).data = data;
(*root).left = leftNode;
(*root).right = rightNode;
(*root).isThreadRight = isThreadRight;
return root;
}
// 후속자 노드를 반환하는 연산
struct treeThNode* findThreadSuccessor(struct treeThNode* p) {
struct treeThNode* q = (*p).right;
if (q == NULL) return q;
if ((*p).isThreadRight == 1) return q;
while ((*q).left != NULL) q = (*q).left;
return q;
}
// 스레드 이진 트리의 중위 순회
void threadInorder(struct treeThNode* root) {
struct treeThNode* q = root;
while ((*q).left) q = (*q).left; // 가장 왼쪽 노드로 이동
do {
printf("%3c", (*q).data); // 현재 노드의 데이터 출력
q = findThreadSuccessor(q); // 후속자 노드 찾기
} while (q);
}
int main(int argc, const char* argv[]) {
// A*B-C/D 수식 이진 트리 만들기
struct treeThNode* n7 = makeRootThNode('D', NULL, NULL, 0);
struct treeThNode* n6 = makeRootThNode('C', NULL, NULL, 1);
struct treeThNode* n5 = makeRootThNode('B', NULL, NULL, 1);
struct treeThNode* n4 = makeRootThNode('A', NULL, NULL, 1);
struct treeThNode* n3 = makeRootThNode('/', n6, n7, 0);
struct treeThNode* n2 = makeRootThNode('*', n4, n5, 0);
struct treeThNode* n1 = makeRootThNode('-', n2, n3, 0);
(*n4).right = n2; // 노드 n4의 오른쪽 서브 트리를 n2로 연결
(*n5).right = n1; // 노드 n5의 오른쪽 서브 트리를 n1로 연결
(*n6).right = n3; // 노드 n6의 오른쪽 서브 트리를 n3로 연결
printf("\n 스레드 이진 트리의 중위 순회 :");
threadInorder(n1); // 스레드 이진 트리의 중위 순회 수행
getchar();
return 0;
}
----------------------------------------------
스레드 이진 트리의 중위 순회 : A * B - C / D2023.11.10 - [알고리즘] - [알고리즘] 트리 2
[알고리즘] 트리2 - 이진 트리의 순회
#1 이진트리의 순회 이진트리의 순회 개념 순회(Traversal)란 모든 원소를 하나라도 빠트리거나 중복하지 않고 처리하는 연산을 의미한다. 리스트, 스택, 큐 등과 같은 선형 자료구조는 원소를 1:1
sun-dori.tistory.com
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘] 트리5 - 균형 이진 탐색 트리(AVL) (0) | 2023.11.14 |
|---|---|
| [알고리즘] 트리4 - 이진 탐색 트리 (0) | 2023.11.13 |
| [알고리즘] 트리2 - 이진 트리의 순회 (0) | 2023.11.10 |
| [알고리즘] 트리1 - 트리와 이진트리 (2) | 2023.11.03 |
| [알고리즘] 연결리스트 스택 구현(자료구조6) (0) | 2023.09.17 |