목차
2023.11.13 - [알고리즘] - [알고리즘] 트리 4 - 이진 탐색 트리
[알고리즘] 트리4 - 이진 탐색 트리
이진 탐색 트리 이진트리는 트리를 효율적으로 구현하고 관리하기 위해서 일정한 조건으로 정의한 것이며, 이진트리를 탐색용 자료구조로 사용하기 위해 원소 크기에 따라 노드 위치를 정해둔
sun-dori.tistory.com
균형 이진 탐색 트리
이진 탐색 트리에서 좌우 균형이 올바르다면 탐색을 할 때 성능이 좋고 이 성능은 탐색 트리의 높이와 밀접한 상관관계를 가진다.
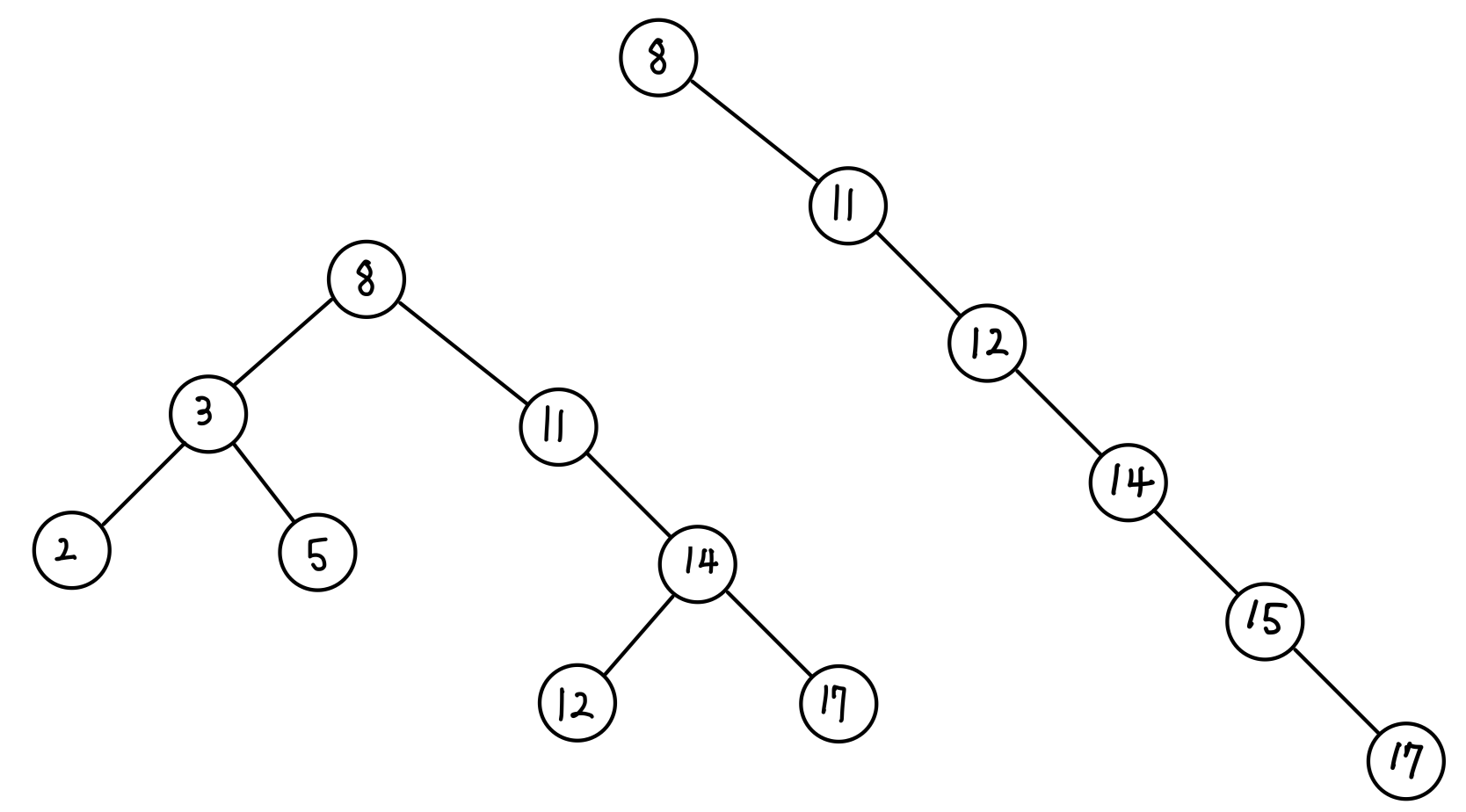
높이가 3인 (a) 트리에서는 17을 탐색하려면 루트 노드 8에서 비교 연산을 4번을 수행해야 하지만...
높이가 5인 (b) 트리에서는 17을 탐색하려면 (a) 트리보다 더 많은 비교 연산이 필요하다..
n개의 노드를 가진 이진 탐색 트리에서 비교 연산 횟수는 최소 높이를 가진 경우에는 $0(\log_{2} n)$가 되지만... (b) 같은 트리의 최고 높이를 가진 트리는 $0(n)$이 된다. 따라서 한쪽으로 치우치지 않고 균형을 이루도록 맞춰주면 탐색 성능을 높일 수 있다.
이러한 원리로 균형 조건을 추가한 트리를 균형 이진 탐색 트리(Balanced Binary Search Tree) 또는 균형 트리(Balanced Tree)라 함.
AVL 트리의 개념과 유형
이 트리는 Adelson-Velskii. Landis Tree의 줄임말인데 그냥 아델슨 아저씨와 란디스 아저씨가 제안한 대표적인 균형 이진트리이다.
각 노드에서 왼쪽 서브 트리의 높이 hL( height of Left subtree )과 오른쪽 서브 트리의 높이 hR( height of Right subtree )의 차이가 1 이하인 균형 트리로서 밑에와 같은 특징을 가진다.
- 왼쪽 서브 트리 < 부모 노드 < 오른쪽 서브 트리 순의 크기 관계를 가진다.
- 각 노드의 왼쪽 서브 트리 높이와 오른쪽 서브 트리 높이의 차이 (hL-hR)인 노드의 균형 인수(BF: Balance Factor)를 관리한다.
- 각 노드의 균형 인수로 {-1, 0, +1}의 값만 가지게 해서 왼쪽 서브 트리와 오른쪽 서브 트리의 균형을 유지한다.
BF = hL - hR

AVL 트리의 회전 연산
| 불균형의 유형과 원인 | 해결 방법 |
| LL유형: 불균형 발생 노드의 왼쪽 자식 노드와 자식의 왼쪽 사직 노드에 의해 왼쪽으로 치우친 현상. | LL회전: 치우친 구간 중 상위 구간을 오른쪽으로 회전 |
| RR유형: 불균형 발생 노드의 오른쪽 자식 노드와 자식의 오른쪽 자식 노드에 의해 오른쪽으로 치우친 현상. | RR회전: 치우친 구간 중 상위 구간을 왼쪽으로 회전 |
| LR유형: 불균형 발생 노드의 왼쪽 자식 노드와 자식의 오른쪽 자식 노드에 의해 왼족 서브 트리가 치우친 현상 | LR회전: 치우친 구간 중 하위 구간을 왼쪽으로 1차 회전 후 2차적으로 LL회전을 적용 |
| RL유형: 불균형 발생 노드의 오른쪽 자식 노드와 자식의 왼쪽 자식 노드에 의해 오른쪽 서브 트리가 치우친 현상 | RL회전: 치우친 구간 중 하위 구간을 오른쪽으로 1차 회전 후 2차적으로 RR회전을 적용 |
LL 회전 연산
LL 회전 또는 Left_Left 회전은 삽입/삭제 연산 후에 AVL 트리에 불균형이 생겼을 때 적용하는데...

// LL 회전
treeNode* LL_rotate(treeNode* parent) {
treeNode* child = parent->left; // 부모의 왼쪽 자식을 가져온다.
parent->left = child->right; // 부모의 왼쪽 자식을 child의 오른쪽 자식으로 연결
child->right = parent; // child의 오른쪽 자식을 부모로 만든다.
return child; // 회전된 서브트리의 새로운 루트 노드인 child를 반환
}RR 회전 연산
RR 회전 또는 Right_Right 회전은 삽입/삭제 연산 후에 AVL 트리에 불균형이 생겼을 때 적용하는데...

// RR 회전
treeNode* RR_rotate(treeNode* parent) {
treeNode* child = parent->right; // 부모의 오른쪽 자식을 가져온다.
parent->right = child->left; // 부모의 오른쪽 자식을 child의 왼쪽 자식으로 연결
child->left = parent; // child의 왼쪽 자식을 부모로 만든다.
return child; // 회전된 서브트리의 새로운 루트 노드인 child를 반환
}LR 회전 연산
LR 회전 또는 Left_Right 회전은 삽입/삭제 연산 후에 AVL 트리에 불균형이 생겼을 때 적용하는데...

// LR 회전
treeNode* LR_rotate(treeNode* parent) {
treeNode* child = parent->left; // 부모의 왼쪽 자식을 가져온다
parent->left = RR_rotate(child); // 왼쪽 자식에 RR 회전을 적용하여 균형을 잡는다
return LL_rotate(parent); // 부모 노드에 LL 회전을 적용하여 균형을 잡고 새로운 루트를 반환
}RL 회전 연산
RL 회전 또는 Right_Left 회전은 삽입/삭제 연산 후에 AVL 트리에 불균형이 생겼을 때 적용하는데...

// RL 회전
treeNode* RL_rotate(treeNode* parent) {
treeNode* child = parent->right; // 부모의 오른쪽 자식을 가져온다
parent->right = LL_rotate(child); // 오른쪽 자식에 LL 회전을 적용하여 균형을 잡는다
return RR_rotate(parent); // 부모 노드에 RR 회전을 적용하여 균형을 잡고 새로운 루트를 반환
}AVL 트리의 구현
본 코드는 이진 탐색 트리(BST)와 균형 이진 탐색 트리(AVL)의 연산 횟수를 비교하기 위해 작성하였다.
#pragma once
#include <stdio.h>
#include <stdlib.h>
#define MAX(a,b) ((a>b)?a:b)
typedef int element; // 이진 탐색 트리 element의 자료형 정의
typedef struct treeNode {
element key; // 노드에 저장될 키 값
struct treeNode* left; // 왼쪽 서브트리를 가리키는 포인터
struct treeNode* right; // 오른쪽 서브트리를 가리키는 포인터
} treeNode;
// LL 회전
treeNode* LL_rotate(treeNode* parent) {
treeNode* child = parent->left; // 부모의 왼쪽 자식을 가져옵니다.
parent->left = child->right; // 부모의 왼쪽 자식을 child의 오른쪽 자식으로 연결
child->right = parent; // child의 오른쪽 자식을 부모로 만듭니다.
return child; // 회전된 서브트리의 새로운 루트 노드인 child를 반환
}
// RR 회전
treeNode* RR_rotate(treeNode* parent) {
treeNode* child = parent->right; // 부모의 오른쪽 자식을 가져옵니다.
parent->right = child->left; // 부모의 오른쪽 자식을 child의 왼쪽 자식으로 연결
child->left = parent; // child의 왼쪽 자식을 부모로 만듭니다.
return child; // 회전된 서브트리의 새로운 루트 노드인 child를 반환
}
// LR 회전
treeNode* LR_rotate(treeNode* parent) {
treeNode* child = parent->left; // 부모의 왼쪽 자식을 가져온다
parent->left = RR_rotate(child); // 왼쪽 자식에 RR 회전을 적용하여 균형을 잡는다
return LL_rotate(parent); // 부모 노드에 LL 회전을 적용하여 균형을 잡고 새로운 루트를 반환
}
// RL 회전
treeNode* RL_rotate(treeNode* parent) {
treeNode* child = parent->right; // 부모의 오른쪽 자식을 가져온다
parent->right = LL_rotate(child); // 오른쪽 자식에 LL 회전을 적용하여 균형을 잡는다
return RR_rotate(parent); // 부모 노드에 RR 회전을 적용하여 균형을 잡고 새로운 루트를 반환
}
// 높이 반환
int getHeight(treeNode* p) {
int height = 0;
if (p != NULL) height = MAX(getHeight(p->left), getHeight(p->right)) + 1; // 노드의 높이를 재귀적으로 계산
return height;
}
// 균형 인수(Balance Factor) 반환
int getBF(treeNode* p) {
if (p == NULL) return 0;
return getHeight(p->left) - getHeight(p->right); // 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 반환
}
// 균형 잡기
treeNode* rebalance(treeNode** p) {
int BF = getBF(*p); // 노드의 균형 인수를 가져온다
if (BF > 1) { // 왼쪽 서브트리가 오른쪽 서브트리보다 높게 나타날 때
if (getBF((*p)->left) > 0)
*p = LL_rotate(*p); // LL 회전을 적용
else *p = LR_rotate(*p); // LR 회전을 적용
}
else if (BF < -1) { // 오른쪽 서브트리가 왼쪽 서브트리보다 높게 나타날 때
if (getBF((*p)->right) < 0)
*p = RR_rotate(*p); // RR 회전을 적용
else *p = RL_rotate(*p); // RL 회전을 적용
}
return *p; // 새로운 루트 노드를 반환
}
// AVL 트리에 노드 삽입
treeNode* insertAVLNode(treeNode** root, element x) {
if (*root == NULL) {
*root = (treeNode*)malloc(sizeof(treeNode));
(*root)->key = x;
(*root)->left = NULL;
(*root)->right = NULL;
}
else if (x < (*root)->key) {
(*root)->left = insertAVLNode(&((*root)->left), x); // 왼쪽 서브트리에 삽입하고 균형을 잡는다
*root = rebalance(root);
}
else if (x > (*root)->key) {
(*root)->right = insertAVLNode(&((*root)->right), x); // 오른쪽 서브트리에 삽입하고 균형을 잡는다
*root = rebalance(root);
}
else {
printf("\n 중복된 값이 존재합니다!\n");
exit(1);
}
return *root; // 새로운 루트 노드를 반환
}
// 이진 탐색 트리에서 노드 탐색
treeNode* searchBST(treeNode* root, element x) {
treeNode* p;
int count = 0;
p = root;
while (p != NULL) {
count++;
if (x < p->key) p = p->left;
else if (x == p->key) {
printf("%3d회 검색 : 키를 찾았습니다.", count);
return p;
}
else p = p->right;
}
count++;
printf("%3d회 검색 : 키를 찾지 못했습니다.", count);
return p;
}
// 이진 탐색 트리에 노드 삽입
treeNode* insertBSTNode(treeNode* p, element x) {
treeNode* newNode;
if (p == NULL) {
newNode = (treeNode*)malloc(sizeof(treeNode));
newNode->key = x;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
else if (x < p->key) p->left = insertBSTNode(p->left, x);
else if (x > p->key) p->right = insertBSTNode(p->right, x);
else printf("\n 중복된 값이 존재합니다!\n");
return p;
}
// 이진 탐색 트리에서 노드 삭제
void deleteBSTNode(treeNode* root, element key) {
treeNode* parent, * p, * succ, * succ_parent;
treeNode* child;
parent = NULL;
p = root;
while ((p != NULL) && (p->key != key)) { // 키를 찾거나 리프 노드까지 이동
parent = p;
if (key < p->key) p = p->left;
else p = p->right;
}
// 키가 존재하지 않을 때
if (p == NULL) {
printf("\n 키가 존재하지 않습니다.");
return;
}
// 리프 노드 삭제
if ((p->left == NULL) && (p->right == NULL)) {
if (parent != NULL) {
if (parent->left == p) parent->left = NULL;
else parent->right = NULL;
}
else root = NULL;
}
// 자식이 하나인 노드 삭제
else if ((p->left == NULL) || (p->right == NULL)) {
if (p->left != NULL) child = p->left;
else child = p->right;
if (parent != NULL) {
if (parent->left == p) parent->left = child;
else parent->right = child;
}
else root = child;
}
// 자식이 둘인 노드 삭제
else {
succ_parent = p;
succ = p->left;
while (succ->right != NULL) { // 왼쪽 서브트리에서 가장 큰 값을 찾는다.
succ_parent = succ;
succ = succ->right;
}
if (succ_parent->left == succ) succ_parent->left = succ->left;
else succ_parent->right = succ->left;
p->key = succ->key;
p = succ;
}
free(p); // 노드 메모리 해제
}
// 중위 순회로 노드 출력
void displayInorder(treeNode* root) {
if (root) {
displayInorder(root->left);
printf("%d_", root->key); // 노드의 키를 출력
displayInorder(root->right);
}
}
int main(void) {
treeNode* root_AVL = NULL;
treeNode* root_BST = NULL;
//////////////////////////////////////////////////////////////////
root_AVL = insertAVLNode(&root_AVL, 50); // AVL 트리 만들기
insertAVLNode(&root_AVL, 60);
insertAVLNode(&root_AVL, 70);
insertAVLNode(&root_AVL, 90);
insertAVLNode(&root_AVL, 80);
insertAVLNode(&root_AVL, 75);
insertAVLNode(&root_AVL, 73);
insertAVLNode(&root_AVL, 72);
insertAVLNode(&root_AVL, 78);
printf("\n ******* AVL 트리 출력 ****************** \n\n");
displayInorder(root_AVL); //중위순회 경로 출력
printf("\n\n AVL 트리에서 70 탐색 : ");
searchBST(root_AVL, 70);
printf("\n\n AVL 트리에서 72 탐색 : ");
searchBST(root_AVL, 72);
printf("\n\n AVL 트리에서 76 탐색 : ");
searchBST(root_AVL, 76);
/////////////////////////////////////////////////////////////////////////////
root_BST = insertBSTNode(root_BST, 50); //BST 만들기
insertBSTNode(root_BST, 60);
insertBSTNode(root_BST, 70);
insertBSTNode(root_BST, 90);
insertBSTNode(root_BST, 80);
insertBSTNode(root_BST, 75);
insertBSTNode(root_BST, 73);
insertBSTNode(root_BST, 72);
insertBSTNode(root_BST, 78);
printf("\n\n\n ******* BST 출력 ************************ \n\n");
displayInorder(root_BST); //중위순회 경로 출력
printf("\n\n BST에서 70 탐색 : ");
searchBST(root_BST, 70);
printf("\n\n BST에서 72 탐색 : ");
searchBST(root_BST, 72);
printf("\n\n BST에서 76 탐색 : ");
searchBST(root_BST, 76);
getchar(); return 0;
}
--------------------------------------------------
******* AVL 트리 출력 ******************
50_60_70_72_73_75_78_80_90_
AVL 트리에서 70 탐색 : 1회 검색 : 키를 찾았습니다.
AVL 트리에서 72 탐색 : 4회 검색 : 키를 찾았습니다.
AVL 트리에서 76 탐색 : 5회 검색 : 키를 찾지 못했습니다.
******* BST 출력 ************************
50_60_70_72_73_75_78_80_90_
BST에서 70 탐색 : 3회 검색 : 키를 찾았습니다.
BST에서 72 탐색 : 8회 검색 : 키를 찾았습니다.
BST에서 76 탐색 : 8회 검색 : 키를 찾지 못했습니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 1 - 그래프의 개념 (1) | 2023.12.05 |
|---|---|
| [알고리즘] 트리6 - 히프 트리(Heap) (2) | 2023.11.20 |
| [알고리즘] 트리4 - 이진 탐색 트리 (0) | 2023.11.13 |
| [알고리즘] 트리3 - 스레드 이진 트리 (1) | 2023.11.13 |
| [알고리즘] 트리2 - 이진 트리의 순회 (0) | 2023.11.10 |