목차
정렬
병합 정렬 Merge Sort
병합 정렬은 여러 개의 정렬된 자료 집합을 병합하여 하나의 정렬된 집합으로 만드는 정렬 방법이다.
이러한 방법은 전체 원소에 대해 수행하지 않고 부분집합으로 분할 Divide 하고 각 부분 집합에 대해서 정렬 작업을 정복 Conquer 즉, 완성한 후에 정렬된 부분집합들을 다시 결합 Combine 하는 분할 정복 Divide and Conquer 기법을 사용한다.
n개의 정렬된 자료 집합을 결합하여 하나의 집합으로 만드는 병합 방법을 n-way라고 한다. 여기서 우리는 두 개의 집합을 하나의 집합으로 만들기에 2-way 병합이라 한다.
다음 3가지의 작업을 반복한다.
- 분할 : 자료들을 두 개의 부분집합으로 분할한다
- 정복 : 부분집합에 있는 원소를 정렬한다.
- 결합 : 정렬된 부분집합들을 하나의 집합으로 정렬하여 결합한다.
첫 번째 단계: 배열을 반으로 나누기
- 배열: {69, 10, 30, 2, 16, 8, 31, 22}
- 배열을 반으로 나누어 각각을 정렬하기 위해 재귀 호출을 수행합니다.
- 왼쪽 배열: {69, 10, 30, 2} / 오른쪽 배열: {16, 8, 31, 22}

두 번째 단계: 각각의 배열을 정렬 (재귀 호출)
- 왼쪽 배열: {69, 10, 30, 2}
- 오른쪽 배열: {16, 8, 31, 22}
- 왼쪽 배열을 반으로 나누기 | 오른쪽 배열을 반으로 나누기:
{69, 10}와 {30, 2} {16, 8}와 {31, 22}

세 번째 단계: 더 이상 나눌 수 없을 때, 배열을 합치면서 정렬
- 나누어진 배열들을 합치면서 정렬합니다.
- 왼쪽 배열 합치기: {10, 69}와 {2, 30}을 합치면서 정렬
결과: {2, 10, 30, 69}
오른쪽 배열 합치기: {8, 16}와 {22, 31}을 합치면서 정렬
결과: {8, 16, 22, 31}


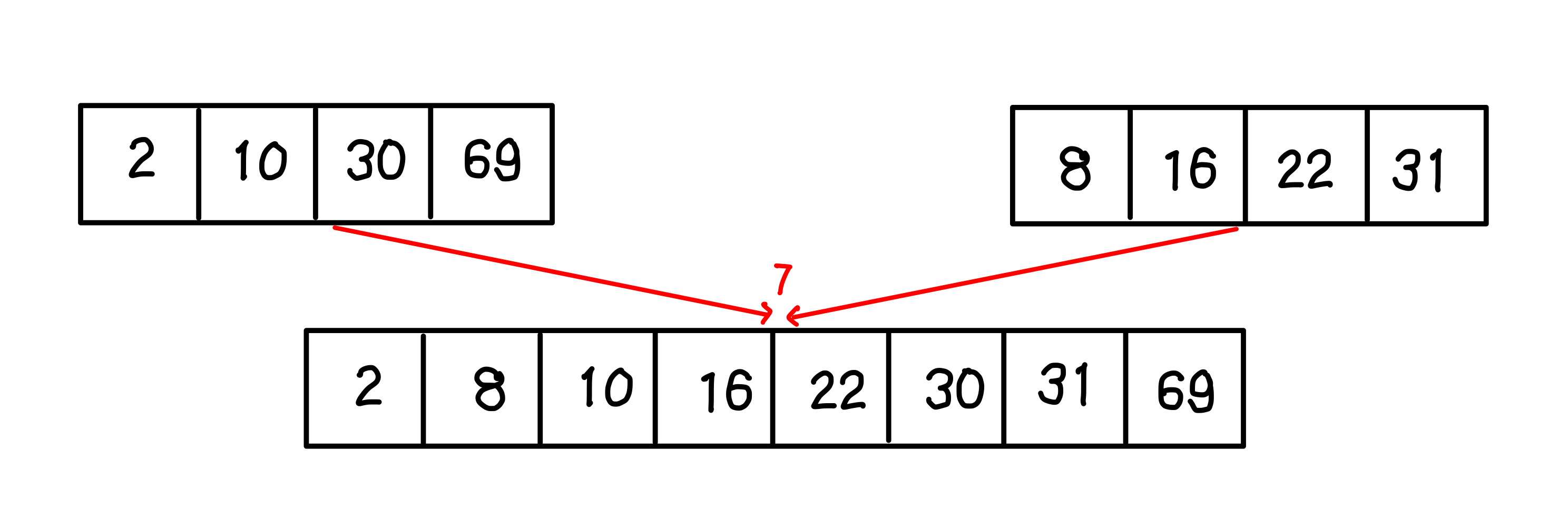
네 번째 단계: 왼쪽과 오른쪽 배열을 합치면서 최종 정렬
- 왼쪽과 오른쪽 배열을 합치면서 최종적으로 정렬된 배열을 얻습니다.
- 왼쪽 배열: {2, 10, 30, 69}
오른쪽 배열: {8, 16, 22, 31}
최종 결과: {2, 8, 10, 16, 22, 30, 31, 69}
#include <stdio.h>
#define MAX 30
extern int size;
int sorted[MAX]; // 원소를 병합하면서 정렬한 상태로 저장할 배열 선언
void merge(int a[], int m, int middle, int n) {
int i, j, k, t;
i = m; // 첫 번째 부분집합의 시작 위치 설정
j = middle + 1; // 두 번째 부분집합의 시작 위치 설정
k = m; // 배열 sorted에 정렬된 원소를 저장할 위치 설정
while (i <= middle && j <= n) {
if (a[i] <= a[j])
sorted[k++] = a[i++];
else
sorted[k++] = a[j++];
} // while
if (i > middle)
for (t = j; t <= n; t++, k++) sorted[k] = a[t];
else
for (t = i; t <= middle; t++, k++) sorted[k] = a[t];
for (t = m; t <= n; t++) a[t] = sorted[t];
printf("\n 병합 정렬 >> ");
for (t = 0; t < size; t++) printf("%4d ", a[t]);
}
void mergeSort(int a[], int m, int n) {
int middle;
if (m < n) {
middle = (m + n) / 2;
mergeSort(a, m, middle); // 앞 부분에 대한 분할 작업 수행
mergeSort(a, middle + 1, n); // 뒷 부분에 대한 분할 작업 수행
merge(a, m, middle, n); // 부분집합에 대하여 정렬과 병합 작업 수행
}
}
int size;
int main(void) {
int i, list[8] = { 69, 10, 30, 2, 16, 8, 31, 22 };
size = sizeof(list) / sizeof(list[0]); // list 배열의 원소 개수
printf("\n 정렬할 원소 >> ");
for (i = 0; i < size; i++) printf("%4d ", list[i]);
printf("\n\n<<<<<<<<<< 병합 정렬 수행 >>>>>>>>>>\n");
mergeSort(list, 0, size - 1); // 병합 정렬 함수 호출
getchar(); return 0;
}
---------------------------------------------
정렬할 원소 >> 69 10 30 2 16 8 31 22
<<<<<<<<<< 병합 정렬 수행 >>>>>>>>>>
병합 정렬 >> 10 69 30 2 16 8 31 22
병합 정렬 >> 10 69 2 30 16 8 31 22
병합 정렬 >> 2 10 30 69 16 8 31 22
병합 정렬 >> 2 10 30 69 8 16 31 22
병합 정렬 >> 2 10 30 69 8 16 22 31
병합 정렬 >> 2 10 30 69 8 16 22 31
병합 정렬 >> 2 8 10 16 22 30 31 69이러한 병합 정렬의 시간복잡도 : O(n log n)로서 부분 집합의 원소를 비교하면서 병합하는 단계에서 최대 n번의 비교 연산을 수행한다.
따라서 각 단계에서 새로 병합하여 만든 부분집합을 저장할 sorted[] 공간이 추가로 필요하기 때문에 정렬할 원소 n개에 대해서 2 x n개의 메모리 공간을 사용한다.
728x90
'알고리즘' 카테고리의 다른 글
| [알고리즘] 정렬 6 - 히프 정렬 Heap Srot, 트리 정렬 Tree Sort (0) | 2023.12.09 |
|---|---|
| [알고리즘] 정렬 5 - 기수 정렬 Radix Sort (0) | 2023.12.09 |
| [알고리즘] 정렬 3 - 삽입정렬, 셸 정렬 (0) | 2023.12.09 |
| [알고리즘] 정렬 2 - 선택 정렬, 버블 정렬, 퀵 정렬 (0) | 2023.12.09 |
| [알고리즘] 정렬 1 (1) | 2023.12.08 |